Beyond Metcalfe's Law to the Power of Community Building
by David P. Reed (https://www.deepplum.com/contactinfo)
[Note: an earlier version of this essay was prepared
as an online supplement to an article in Context magazine published in
Spring 1999]
Bob Metcalfe, inventor of the Ethernet, is known for
pointing out that the total value of a communications network grows with the
square of the number of devices or people it connects. This scaling law, along
with Moore's Law, is widely credited as the stimulus that has driven the
stunning growth of Internet connectivity. Because Metcalfe's law implies value
grows faster than does the (linear) number of a network's access points, merely
interconnecting two independent networks creates value that substantially
exceeds the original value of the unconnected networks. Thus the growth of
Internet connectivity, and the openness of the Internet, are driven by an
inexorable economic logic, just as the interconnection of the telephone network
was forced by AT&T's long distance strategy. This strategy created huge and
increasing value to AT&T customers, based on the same (then unnamed) law of
increasing returns to scale at the beginning of the 20th century. In the same
way, the global interconnection of networks we call the Internet has created
huge and increasing value to all its participants.
But many kinds of value are created within networks. While many kinds of value grow proportionally to network size and some grow proportionally to the square of network size, I've discovered that some network structures create total value that can scale even faster than that. Networks that support the construction of communicating groups create value that scales exponentially with network size, i.e. much more rapidly than Metcalfe's square law. I will call such networks Group-Forming Networks, or GFNs.
Even if it's not your business to supply communications services, your business participates in many networks—perhaps the most important are supply networks that allows access to and bidding among suppliers and distribution networks that allows access to and competition among customers. The structure of these networks or market spaces, especially the value of the connectivity and relationships produced in these networks, can play a crucial role in defining the value of your business. If you can manage or influence the networks that connect you to suppliers and customers to create more value for all concerned, that extra value can be used as a competitive weapon. So paying attention to network value is a crucial strategic issue, especially as businesses move their customer and supplier relationships into the 'net.
What kind of value are we talking about, when we say the value of a network scales as some function of size? The answer is the value of potential connectivity for transactions. That is, for any particular access point (user), what is the number of different access points (users) that can be connected or reached for a transaction when the need arises. As a simple illustration, consider a phone that can call only 911. A customer for such a phone buys it because of a low probability future need to call for emergency help; in fact, the customer probably takes other steps never to need to use the phone. But the existence of a lucrative market for such phones indicates that customers can value potential connectivity to a single point, even though the connection is never used. Potential connectivity to many points should have value proportionally larger, since it is not necessary to use the connection to find value in its availability.
The value of potential connectivity is the value of the set of optional transactions that are afforded by the system or network. Economically, the value of each optional transaction is like a financial option (e.g., the value of an option to buy a share of stock at a particular price). To simplify the model and focus on scaling, I'll assume that the value of any particular optional transaction in a network comes from a distribution that does not depend strongly on the number of participants in the network.
Metcalfe's law, simply derived, says that if you build a network so that any customer can choose to transact with any other customer, the number of potential connections each of the N customers can make is (N-1), giving a total number of potential connections as N(N-1) or N2-N. Assuming each potential connection is worth as much as any other, the value to each user depends on the total size of the network, and the total value of potential connectivity scales much faster than the size of the network, proportional to N2.
At this point a skeptic once said to me, that's too simplistic, that's not the most important source of value in the network like the phone network. For example, there's a weather service that everyone calls once a day, and the 911 service, and a couple of other services like that. And each user typically has a fixed, small set of friends and family that they call all of the time. Since the value of these services to a particular user does not depend on the number of other users of the network, the total value of these services grows more slowly—proportional to N, not N2.
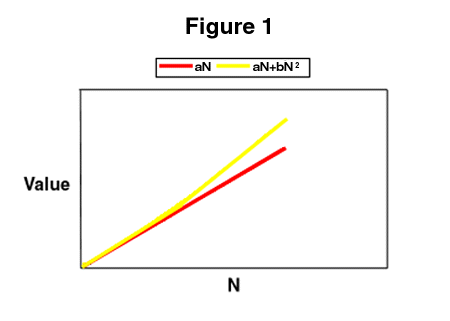
The skeptic was right that some important services scale only linearly, but in drawing his conclusion missed a crucial, very important point about scale and growth. To illustrate this, let's assume that we can lump all of the kinds of value that grow proportional to N in one term, which we can write by the formula aN, where a is a constant that represents the value per customer. We can also represent the value of potential connectivity by bN2, where b is the constant value of a potential connection between a pair of customers. Let's assume that b is much smaller than a, so that for a modest size network, the total network value aN + bN2 is for all intents and purposes the same as aN. But still, if we allow N to get large enough, the total network value will get closer and closer to bN2. Thus, the "square" value of potential connectivity dominates all linear sources of value once N gets sufficiently large. See figure 1, which shows how, when N is small, the total value is approximately linear, but as N gets larger, the total value begins to follow bN2.

This dominance of peer connection value suggests that it is foolish for phone companies to lust after the video rental business in an attempt to compete with cable. As networks get larger, the value of peer connectivity is likely to dominate the combined capability of phone and cable networks. Only when the potential consumers of peer connectivity have been saturated does it seem sensible to go after businesses where value grows linearly with customer base. Of course, the same scaling dominance suggests that cable TV networks ought to do whatever is necessary to enable their systems to support telephony and other transactional services if possible!
But there's an additional, new wrinkle to network scaling. I recently discovered a new value-creation effect that dominates even the remarkable effects of Metcalfe's Law, when a network supports it.
In networks like the Internet, Group Forming Networks (GFNs) are an important additional kind of network capability. A GFN has functionality that directly enables and supports affiliations (such as interest groups, clubs, meetings, communities) among subsets of its customers. Group tools and technologies (also called community tools) such as user-defined mailing lists, chat rooms, discussion groups, buddy lists, team rooms, trading rooms, user groups, market makers, and auction hosts, all have a common theme—they allow small or large groups of network users to coalesce and to organize their communications around a common interest, issue, or goal. Sadly, the traditional telephone and broadcast/cable network frameworks provide no support for groups.
What I found that's surprising and important is that GFNs create a new kind of connectivity value that scales exponentially with N. Briefly, the number of non-trivial subsets that can be formed from a set of N members is 2N-N-1, which grows as 2N. Thus, a network that supports easy group communication has a potential number of groups that can form that grows exponentially with N.
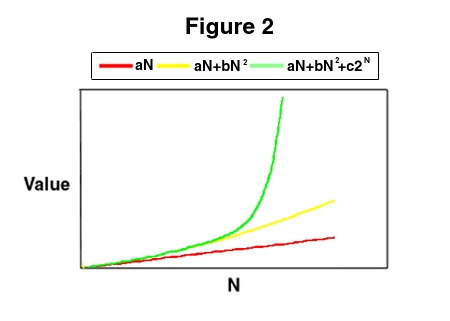
The exponential, 2N, is a sneaky function. Though it may be very small initially, it grows much faster than N2, N3 or any other power law. So if there is any portion of the total network value that grows exponentially, scale effects will eventually bring that value to the fore, where it will dominate any other source of value. (To put it simply, if a network's value consists of components that scale proportional to N, N2, and 2N, we can write the total value as aN + bN2 + c2N where a, b, and c are constants. As long as a, b, and c are positive, there will be some M such that the total value is dominated by the term c2N for all N>M. Even if c is quite small, the exponential will eventually dominate.) See figure 2.
| Law: | Sarnoff | Metcalfe | GFN (Reed) |
| Optional Transactions | Tune In Broadcast | Connect Peers | Join/Create Groups |
| Examples | OnSale, Remote Access |
Yahoo! Classifieds, EMail | eBay, Chat Rooms |
| Value of N member net | N | N2 | 2N |
| Combined Value of N, M member nets | N + M | N2 + M2 + 2NM | 2N x 2M |
This exponential law of GFNs, like Metcalfe's Law, creates increasing returns as scale increases, which has surprising economic results.
Both laws give a powerful bonus to interconnection; mergers and partnerships of networked companies should be able to extract a premium resulting from these laws. When we combine two networks together so that users of one network can connect seamlessly to users of the other, Metcalfe's Law tells us already that substantial new value is created: (M+N)2 = M2 +N2+2MN. This bonus term, 2MN, is substantial-up to 100% of the value in the original unconnected networks. Thus there is an enormous incentive to find ways to interconnect networks, since the members of each network can access a much larger set of potential transaction partners. With the GFN law, interconnection is even more powerful, creating many new potential groups that span the two networks: 2M+N = 2M2N. The GFN interconnection bonus percentage itself grows exponentially with the size of the smaller network.
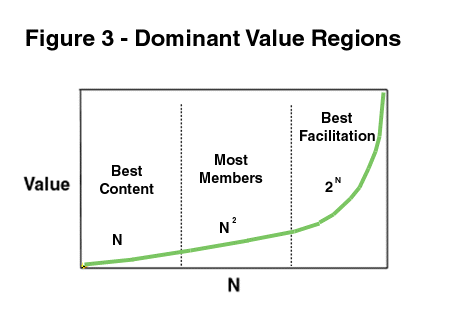
What we see, then, is that there are really at least three categories of value that networks can provide: the linear value of services that are aimed at individual users, the "square" value from facilitating transactions, and exponential value from facilitating group affiliations. What's important is that the dominant value in a typical network tends to shift from one category to another as the scale of the network increases. Whether the growth is by incremental customer additions, or by transparent interconnection, scale growth tends to support new categories of killer apps, and thus new competitive games. See figure 3.
We can see this scale-driven value shift in the history of the Internet. The earliest usage of the Internet was dominated by its role as a terminal network, allowing many terminals to selectively access a small number of costly timesharing hosts. As the Internet grew, much more of the usage and value of the Internet became focused on pairwise exchanges of email messages, files, etc. following Metcalfe's Law. And as the Internet started to take off in the early ' 90's, traffic started to be dominated by "newsgroups" (Internet discussion groups), user created mailing lists, special interest websites, etc., following the exponential GFN law. Though the previously dominant functions did not lose value or decline as the scale of the Internet grew, the value and usage of services that scaled by newly dominant scaling laws grew faster. Thus many kinds of transactions and collaboration that had been conducted outside the Internet became absorbed into the growth of the Internet's functions, and these become the new competitive playing field.
What's important in a network changes as the network scale shifts. In a network dominated by linear connectivity value growth, "content is king." That is, in such networks, there is a small number of sources (publishers or makers) of content that every user selects from. The sources compete for users based on the value of their content (published stories, published images, standardized consumer goods). Where Metcalfe's Law dominates, transactions become central. The stuff that is traded in transactions (be it email or voice mail, money, securities, contracted services, or whatnot) are king. And where the GFN law dominates, the central role is filled by jointly constructed value (such as specialized newsgroups, joint responses to RFPs, gossip, etc.).
In "real" networks, it is important to note that although the total value of optional transactions that involve pairs and groups grows faster than linearly, the total price that can be paid cannot grow that fast. Typically, the consumers of the value have money and attention resources that scale linearly with N. So the law of supply and demand will kick in, lowering prices until the available resources (dollars and attention) are saturated. What's interesting is that this saturation process affects all types of optional transactions-so GFN value, peer transaction value, and broadcast content value all compete for the same resources. Once N grows sufficiently large, GFN transactions create more value per unit of network investment than peer transactions, and peer transactions create more value per unit of network investment than do broadcast transactions. So what tends to happen is that as networks grow, peer transactions out-compete broadcast content in the arena of attention and return on investment. And remarkably, once N gets sufficiently large, GFN transactions will out-compete both of the other categories.
The chart in Figure 4 is based on a simple model of saturation and competition for dollars and attention. As N grows, first peer transactions start to gain "market share" at the cost of broadcast, and the GFN transactions gain share.

Scale driven value shifts will powerfully shape electronic commerce. The Internet auction pioneer, OnSale, is based on a business model that scales linearly, proportionally to the reach of its network. OnSale buys closeout products and auctions them to anyone who can access its website to present a bid. In return, OnSale gets margin on every sale. Online classifieds, which connect buyers to sellers on a peer-to-peer basis, would seem to create a market space whose value follows Metcalfe's Law. We'd expect to see a shift of dominance from OnSale to online classifieds once the network tools for safe peer transactions can be made to work. But the newly public company eBay seems destined to capture a scale shift to the exponential logic of GFNs in creating value for its members. EBay's concept is to help its members to set up specialized auction communities on its website as buyers and sellers of many kinds of collectibles, art, and other easily traded special interest goods. Though eBay's share of the transactions it facilitates is much smaller than OnSale's share, eBay's returns can increase much more rapidly with scale. This growth in returns will be driven by an exponential growth in value of the eBay GFN as its membership increases (and new kinds of jointly constructed value become important-e.g. eBay's origins in creating a market for Pez candy dispenser collectors).
Scale driven value shifts have already caused IBM subsidiary Lotus, the pioneer of enterprise groupware, to incorporate features into Notes/Domino to interconnect in a limited way with the faster-growing Internet. But Notes' enterprise focus makes it difficult to support ad hoc groups that live outside large enterprise boundaries or span multiple enterprises. Though the email capabilities of Notes can easily interconnect with other Internet email systems across boundaries to capture a fair share of Metcalfe's Law value as the Internet grows, Lotus has chosen an enterprise-oriented model for sales and an enterprise focused security model. That choice effectively limits GFN reach to a few islands scattered throughout a vast Internet. Thus scale driven value seems likely to shift dominance to new groupware products and business models that can capture exponential value growth by enabling all Internet users to affiliate flexibly. By facilitating easy ad hoc creation of "teamrooms", Instinctive's eRoom and Excite's Excite Communities, among others, seem likely to capture big shares of a scale driven value shift from email to ad hoc project team collaboration.
As digital networking brings scale and global reach to all aspects of our lives and activities, there will be many more ways that we'll see scale driven value shifts that threaten established business networking patterns. For example, health care networks may move from treatment transactions to collaborations around disease management. Risk management in the financial services sector may move to group-forming structures that facilitate management of "micro-risks". How will it impact your business and your industry?
I'd like to close with a speculative thought. As Francis Fukuyama argues in his book Trust, there is a strong correlation between the prosperity of national economies and social capital, which he defines culturally as the ease with which people in a particular culture can form new associations. There is a clear synergy between the sociability that Fukuyama discusses and the technology and tools that support GFNs-both are structural supports for association. As the scale of interaction grows more global via the Internet, isn't it possible that a combination of social capital and GFN capital will drive prosperity to those who recognize the value of network structures that support free and responsible association for common purposes?
For further information
I've begun assembling a collection of materials related to the concept of Group Forming Networks on my website. Feel free to explore it at https://www.deepplum.com/gfn